Proving Divisibility Tests for 3, 9 and (b-1)
A well-known method of testing if an integer is divisible by 3 is to sum its digits – if the resulting value is a multiple of 3, then the integer itself is also divisible by 3. Moreover, this method also works for testing if a number is divisible by 9 (but instead of checking to see if the digit sum is a multiple of 3, we check to see if it is a multiple of 9). This technique does not work for higher powers of 3..
You can use it with GitLab Pages as well as a standalone project.
Proving that these divisibility tests always work is a relatively simple endeavour: we must first consider the ways we can represent an integer x in base 10 – clearly, simply writing the integer out as a single value is one way. However, given that we are concentrating on properties of the digit sum of x, it would be helpful if we could represent x in terms of its digit sum. Any integer in base 10 can be written as a series of multiples of powers of 10, for example, the number 164 is equal to a single 100, plus 6 times 10 and 4 times 1 (which is 10 to the power of 0). We can see that the coefficients of these powers of 10 are the digits of the integer x. So, if we define x to be an arbitrary integer in base 10 with n digits (where n is also an arbitrary integer), we can write x and its digit sum in the manner below:
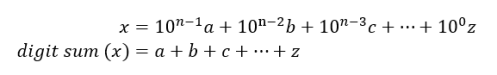
Now, consider what happens when the digit sum is subtracted from x:
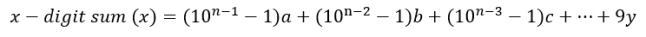
Since 10 is congruent to 1 modulo 3, any power of 10 is immediately made a direct multiple of 3 if 1 is subtracted from it, so we can conclude that the difference between any base 10 integer x and its digit sum is a multiple of 3 (since all of the coefficients of the digits in the value above are all multiples of 3). Clearly, this means that x and its digit sum must always be congruent to the same value modulo 3, and thus if the digit sum of x is congruent to 0 modulo 3 (that is, the digit sum of x is a direct multiple of 3), then x itself must also be a direct multiple of 3. In other words, for the difference between two values to be a multiple of 3, the two values must always give the same remainder when divided by 3 (as the remainders ‘cancel each other out’ during the subtraction), so therefore if the digit sum of x leaves a remainder 0 when divided by 3, then x itself must do so, too.
Note that 10 is also congruent to 1 modulo 9, so the difference between x and its digit sum must also be a direct multiple of 9, and thus the same logic can also be used to deduce that if the digit sum of x is a direct multiple of 9, then x itself must also be a multiple of 9.
Interestingly, we can also use this logic to generalise a divisibility test for the value β-1 for integers in base β. More formally:
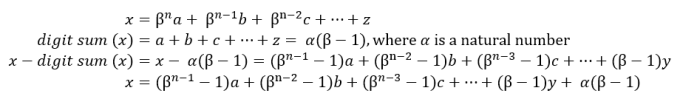
By modular arithmetic, (β – 1) can always be factorised out of (βn – 1) when all values concerned are integers, so, clearly, if the digit sum of x in base β is a direct multiple of β-1, then x can be represented as a summation of direct multiples of β-1 and thus x itself must also be a direct multiple of β-1. Hence proved.