Generating Pythagorean Triples – Euclid’s Formula
In geometry, Pythagorean triples are 3-tuples of integers which satisfy the Pythagorean theorem (that is, the sum of the squares of two of the integers is equal to the square of the third, and thus the values can represent the lengths of the three sides of a right-angled triangle where the largest value is the length of the hypotenuse). In this post, we will explore ways of generating them. Clearly, given a single Pythagorean triple, we can multiply all of its numbers by an integer factor to create a new triple:
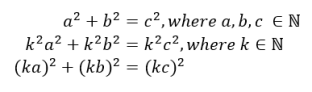
However, a technique of this nature would only find triples which are multiples of other triples – so, we would be unable to use it to find ‘primitive’ triples (that is, triples where two or three of the involved numbers are relatively prime – so we are unable to divide these by a common factor). Euclid’s formula tackles this problem – the technique is to take two relatively prime natural numbers m and n of opposite parity (so one and only one of the two values must contain a factor of 2) and use them to create three positive integers which in turn form a primitive Pythagorean triple:
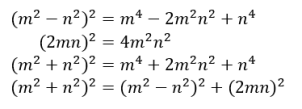
Note that the squares of m and n need to be used for the expressions in parentheses, as we would be forced to take one of the triple’s integers as a product of two square roots if this was not the case. Clearly, this would result in triples which do not exclusively contain whole numbers if one of the square roots is irrational.
We have stated that m and n must be relatively prime and of opposite parity for Euclid’s formula to generate a primitive triple. Why this is the case can be explained elegantly using simple number theory – clearly, if the two integers are not relatively prime, then it will be possible to divide both sides of the last equation shown above by the common factors of m and n to receive whole values (so, by definition, the initially-formed triple could not have been primitive). We can use modular arithmetic to justify why one of m or n must be even – suppose that this was not the case and the two integers are merely both odd and relatively prime:
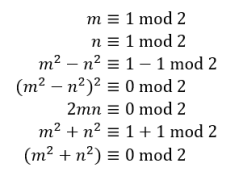
So, we have shown that if both m and n are odd, then the all of the integers generated as part of the triple will have the common factor 2, and thus the triple would not be primitive. For readers unfamiliar with modular arithmetic, this proof revolves around the idea that multiplying two odd numbers together (or squaring an odd number) gives an odd number, adding two odd numbers together gives an even number and multiplying any odd number by 2 gives an even number. Therefore, all three of the expressions used to generate the triple’s integers will give an even number.
Here is a C++ program which generates primitive Pythagorean Triples given two arbitrary values for m and n as input (refer to the comments for a more detailed explanation as to how the code works):
#include
#include
#include
using namespace std;
/* The following data structure represents
* a Pythagorean triple - it holds three integer
* values 'a', 'b' and 'c' which satisfy the Pythagorean
* Theorem in the manner discussed earlier in the post. */
struct PythagoreanTriple {
int a;
int b;
int c;
/* The constructor takes the integer arguments 'sa',
* 'sb' and 'sc' and loads them into their respective
* variables held by the structure. */
PythagoreanTriple (int sa,
int sb,
int sc) {
a = sa;
b = sb;
c = sc;
}
/* The overloaded '<' operator is used by the
* built-in 'sort ()' procedure provided by the C++
* library as a means of comparing two Pythagorean
* triples by their 'a', 'b' and 'c' values. Triples
* are first sorted by their 'a' values, then their 'b'
* values and finally by their 'c' values. */
bool operator < (const PythagoreanTriple& other) const {
if (a < other.a)
return true;
else if (a == other.a && b < other.b)
return true;
else if (a == other.a && b == other.b && c < other.c)
return true;
else
return false;
};
};
/* This is a simple function to test whether two
* integers are relatively prime or not. This is done
* by checking each number from 2 to the smaller of
* the two values and ensuring that each number tested
* cannot divide both 'value1' and 'value2'. */
bool RelativelyPrime (int value1, int value2) {
for (int i = 2; i <= min (value1, value2); i++) {
if (value1 % i == 0 && value2 % i == 0)
return false;
}
return true;
}
int main () {
/* First, the maximum values of 'm'
* and 'n' are taken from the standard input. */
int maxn, maxm;
cin >> maxn >> maxm;
/* We then loop through all possible ordered
* pairs (n, m) and generate primitive Pythagorean
* triples accordingly. When a new triple is created,
* it is stored in the 'triples' vector. */
vector triples;
for (int n = 1; n <= maxn; n++) {
for (int m = n + 1; m <= maxm; m++) {
if ((n != 1 && RelativelyPrime (m, n)) ||
(n == 1 && m % 2 == 0)) {
PythagoreanTriple triple (m * m - n * n,
2 * m * n,
m * m + n * n);
triples.push_back (triple);
}
}
}
/* With the aid of the overloaded '<' operator in
* the 'PythagoreanTriple' structure, the 'sort ()'
* procedure provided by the standard library sorts
* all of the generated triples into ascending order. */
sort (triples.begin (), triples.end ());
/* Finally, we loop through the 'triples' vector and
* print the integers in each triple to the standard output. */
for (int i = 0; i < triples.size (); i++) {
cout << triples[i].a << " " <<
triples[i].b << " " <<
triples[i].c << "\n";
}
return 0;
}
By using the formula discussed earlier, this program generates triples significantly faster than a program which uses three nested loops to test for 3-tuples of integers which satisfy the Pythagorean Theorem. In order for a program of this nature to generate triples containing numbers up to a high power of 10, such as 100000, it would need to perform three nested loops up to this value, forcing an absurdly high number of operations. On the other hand, the program written above only needs to loop through values of n and m in the thousands to achieve values in this range, despite having a similar time complexity.
There are still other ways to further optimise our program, however. Its time complexity could be dramatically improved through the introduction of a more efficient way of determining whether two integers are relatively prime – currently, we perform a linear search of all natural numbers from 2 to the smaller of the two integers in question. This could potentially be done through using the sieve of Eratosthenes to create a list of all of the prime numbers up to a suitably high value and then checking whether the two integers contain any common prime factors. Alternatively, we could use the ‘Euclidean Algorithm’ to find the greatest common divisor of the two integers – if this value is 1, then the integers are clearly relatively prime. Both of these techniques will be explored in future posts.